Cannonballs! Part 3.2


by Robert Cailliau

We know how to move objects around and we know how to debug. Now we have to simulate the cannonball's motion.

Problems of drawing the cannonball's path

The cannon fires a ball at some angle with some speed. As soon as the ball leaves the barrel, it flies on its own. It is no longer pushed by the explosion of the gunpowder. How does it move? Its motion is influenced by gravity and a few other effects.

Effects we will ignore

Air

Apart from gravity there is also wind and resistance of the air. Neither of these can be ignored by real gunmen.

Rotation

The Earth turns counterclockwise when you look down on it from above the north pole. If you are in the northern hemisphere, you are going eastwards around the axis. The closer you are to the pole, the smaller your eastward speed is, and at the pole it is zero. If you fire a ball due north, towards the pole, then it will start with an eastward speed higher than the eastward speed of the ground where it lands: it will fall more to the east than expected (the Coriolis force) (for inhabitants of the southern hemisphere: invert the motions).

Curvature

The force of gravity points towards the centre of the Earth, it is not perpendicular to a flat plane.

We will ignore air resistance, wind, the Earth's rotation and curvature; we will only do gravity.

Why we want to simulate the physics

To draw the trajectory, we could work through the laws of motion, find the equations and draw the mathematical curves. But that's not good for two reasons:

1. We want to see it happen, so we must make the ball move, like in a movie. That's difficult from a pre-calculated equation.
2. If we draw from pre-computed equations and we want to introduce another effect, then we have to redo all our mathematics again.

It's much more instructive to set up the program so that it simulates the effects of the real world step by step. Once for each image of the movie, if you like, and from the motion program we know how to do that now.

Forces and speeds of the cannon ball.

If there were no forces at all, the cannonball would just go straight on forever, at the same speed it had when it left the barrel of the cannon:

The speed is a number v probably something like 400 m/s, a little more than the speed of sound. But v also has a direction! We indicate that by the arrow. The speed has in fact two components: one along the ground and one vertically:

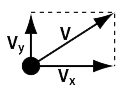
Usually the horizontal axis is called the x-axis and the vertical one the y-axis. That's why we will call the two components vx and vy.

Since we will ignore friction and assume the Earth is flat, then the only force F is gravity. It works perfectly vertically. That means the Vx component of the speed will not be affected: F is perpendicular to it. Gravity is aligned with Vy.

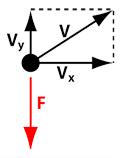
Acceleration is proportional to the force F and it is constant because F is constant. Our simulation therefore looks like this:

1. along the ground the acceleration ax is zero, vx then does not change and the x-coordinate changes by the same amount for each step in the simulation.
2. along the vertical the acceleration ay is constant, then for every step in the simulation changes by the same amount and the y-coordinate changes by something proportional to vyvy.

We can take the repeat from our Motion program and modify it thus:

This needs a lot of detailed attention.

Analysing the simulation loop

I'll write it again, with a number in front of each line:

First note that all statements have doubled up: there is always a statement for the x-component and another one for the y-component. They are very similar but not quite the same. I have put matching statements on the same line.

Line 01 sets the starting position of the canonball, i.e. where the cannonball is when it leaves the barrel. I put dots there: ... simply because we will get those numbers later.

Line 02 tells us with what speed the ball leaves the barrel. Again we will get those numbers later, so I have put dots there too.

Line 03 gives us the acceleration, and at least we know that: it is 0 for the x-component and it works down for the y-component. I chose 1 for the size, but because it works downward, I have to write -1.

Lines 04 and 05 are the same as in the Motion program: they are some constant factors that we will not worry about yet.

Line 06 is also OK for now, and so is the corresponding line 11.

Line 07 just sets the location of the ball, and we know that one too.

Line 08 has the change of the position: once for the x-coordinate and once for the y-coordinate. That too is familiar from the Motion program.

And finally line 09 should also not be a problem.

Except that it is all wrong!

The y-coordinate in these statements is measured upwards, and on the computer screen they should be measured downwards.

For the physics we will use the normal axes system where y points upwards, but for the drawing we will have to use the other one. We can convert because we know what it looks like:

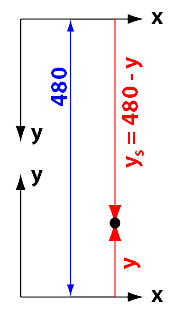
If we start from the grass, where the height y would be zero, then we know that the top of the window is at 480 pixels above that. If we use ys for "the y on the screen" then it is easy to see that ys = 480 - y.

But it is simpler than that! (you may have to think about this for a while, it is not obviou)s
Whatever y value we start out with, we are only changing it: we are modifying it a little. If the physics-y increases by a certain amount, then the screen-y will decrease by exactly the same amount. If the physics-y decreases by a certain amount, then the screen-y will increase by exactly the same amount. It does not matter how far from the top of the window we are, or how far above the grass we are!

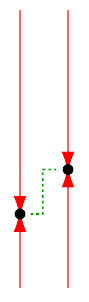
What one gains, the other loses. All we need to do is change line 09:

add lVx*lK1 to lX; subtract lVy*lK1 from lY

And that's it.

We still need to know what to write for the dots.

Powder and trigonometry

The speed with which the cannonball leaves the barrel will be dependent on how much powder we stuff into the barrel and explode. In the next page we will create a scrollbar to set the amount of powder, here we will just call it Powder. Let's look again at the speed diagram:

then the length of the V arrow will be proportional to the amount of powder:

V = Powder * k3

We're used to having these k-numbers, but how do we find the length of the vx and vy arrows? We know the elevation angle:

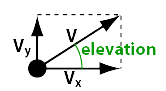
and no matter what the elvation angle is, the length of V will stay the same. The higher the elevation, the shorter vx will become and the longer vy will be. This is however not a proportional transition and it takes us into trigonometry, the art of measuring triangles. I will not explain the trigonometric functions here. They are very important but you will just have to take my word for the use I will make of them:

vx = v * cos(elevation)

vy = v * sin(elevation)

The function cos is pronounced "cosine" and sin is pronounced "sine". Both are mathematical functions that are already present in Transcript so you do not have to worry.

Unfortunately for us, we measure angles in degrees but mathematical functions expect radians. The conversion is simple: 360 degrees (completely around the whole circumference of a circle) corresponds to 2π radians. We know that π is 3.14159... but we don't need to write those digits: Transcript already has π built-in as the word pi. You can use the message box and type put pi to see what it is.

If 360 degrees corresponds to 2*pi then 1 degree corresponds to 2*pi/360 or pi/180 and elevation corresponds to lElevation*pi/180

That gives us the second pair of dots: line 02 becomes

put lPowder*lK3*cos(lElevation*pi/180) into lVx; put lPowder*lK3*sin(lElevation*pi/180) into lVy

I have again followed my naming rules by prefixing a lower case letter l to the names of local variables we invent.

What are the first pair of dots? They are the starting position: the nozzle of the barrel. We do something very similar here as for the speed:

We know the loc of the image BarrelImage and also its width. The nozzle is then up from the centre of the barrel image by half the width times the sine of the elevation, and further right by half the width times the cosine of the elevation. And of course we need to convert the degrees to radians.